Comparing Group Means

Dependent (Paired) t-test

When do you use it?

If you have 1 group that you are testing 2 times (pre-test vs. post test). Used to determine if a treatment worked.

Sample Data

Question: What are the differences in grip strength between the pre-test and posttest? We are testing each individual TWO times.

Pretest: Carpal Tunnel Syndrome patients with no treatment (control)

Posttest: Carpal Tunnel Syndrome patients with treatment (treatment)

In this scenario, if there is a difference BETWEEN THE PRETEST and POSTTEST, but no variance WITHIN THE GROUPS, then all differences can be EXPLAINED by the effect of the treatment.

Variable View:

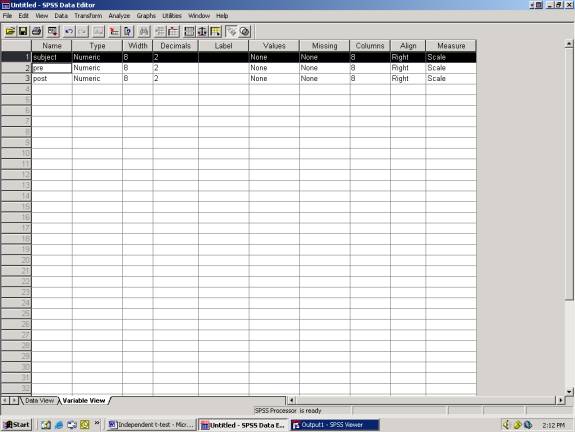
The variables in this example are

1) subject number

2) pre test values

3) post test values

Data View:

Click on Data View

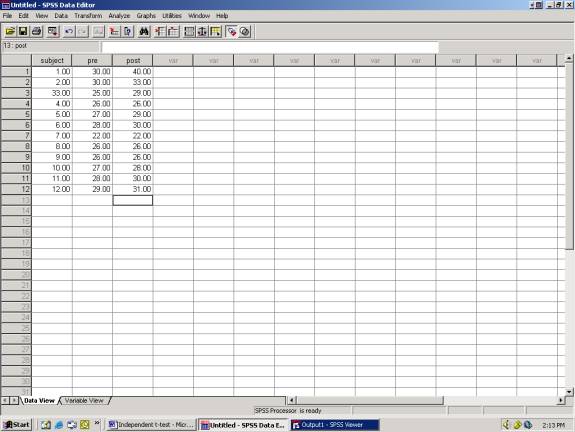
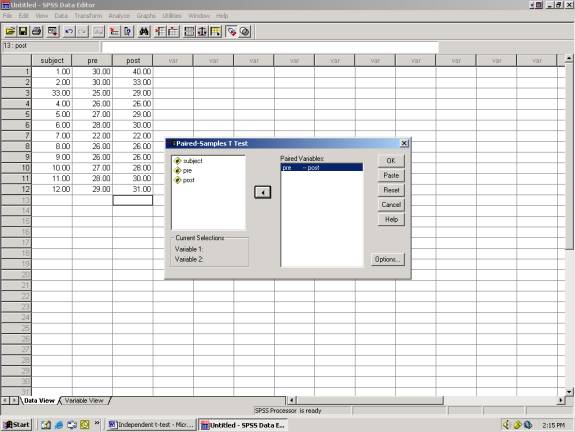
To run paired t-test statistics select:

Analyze

Compare Means

Paired Samples T-Test

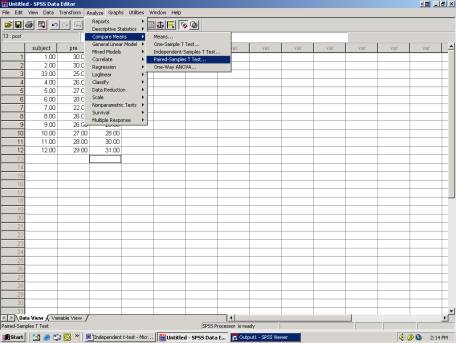
2) Click “post” second and it will appear in Variable 2

3) Click “ok”

1) Click “pre” first and it will appear in Variable 1

After clicking “ok” your statistics will appear.

Mean, number of subjects in each group (N), standard deviation and standard error of mean

5

4

3

2

1

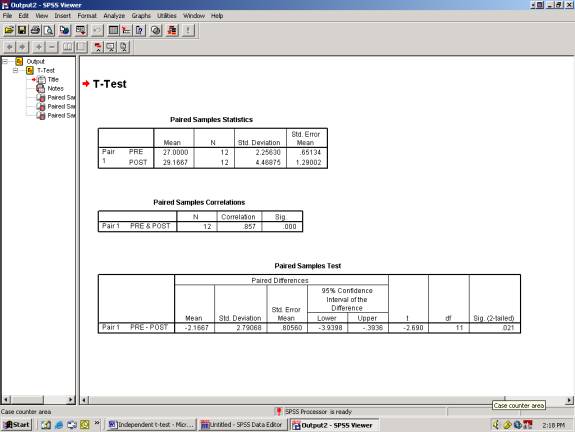
What your statistics mean

1) Is there a correlation between our pre and post test that is significant? In this example, “yes”. Perfect correlations are “1.0” and in our case it is .857 .

a. Normally, correlations ranging from:

0.00- 0.25 indicate little or no relationship

0.25-0.50 a fair degree of relationship

0.50-0.75 are moderate to good

> .75 are good to excellent

2) Mean of the difference scores

3) Standard deviation and standard error mean of the different scores

4) Confidence Intervals. The computer automatically selects a 95% CI. The scores does not contain zero, indicating a significant difference.

5) Two tailed significance. It is less than 0.05 so there is a significant difference in pre and post test scores. This indicates that the treatment works. (If we wanted a one-tailed significance score, then divide by 2.)